این ترم به طور ناباورانه با حالات خاص در ریاضیات مواجه شدم!
ترکیبیات:
مجموعه اعداد طبیعی را با نماد N نمایش میدهند.
مهمترین کاربرد اعداد طبیعی شمردن است.
در ریاضیات نوین و علم مبانی ریاضی اعداد طبیعی به صورت زیر تعریف میگردند :
مجموعه تهی= {} = 0
{ {} } = {0} = 1
{ {{}} ، {} } = {0،1} = 2
{ { {{}} ، {} } ، { {} } ، {} } = {0،1،2} = 3
.
.
{n = {0,1,2,3,…,n-1
طبق اصول کلاسیک نظریه مجموعهها یا ZFC ، تعاریف فوق خوش تعریف هستند.
طبق تعریف فوق اگر و اعداد طبیعی باشند ، 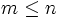 اگر و تنها اگر
اگر و تنها اگر 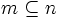 .
.
همان گونه که میبینید در این تعریف عدد صفر نیز عضو مجموعه اعداد طبیعی تعریف شده است.
طبق این تعریف من در سرجلسه ترکیبیات N را از صفر شروع کرده و یک سوال را حل کردم که استاد هم کم نیاورد و صفر به ما داد! (توجیه خوبی بود اما ...)
جبر خطی عددی:
در به دست آوردن مقادیر ویژه این نکته را فراموش کرده بودم!
مقدار ویژه میتواند صفر باشد اما بردار متناظر با مقادیر ویژه نمیتواند صفر باشد!
این جوری که استاد میگفت هیچ کس این حالت رو در نظر نگرفته بود!

 ؟
؟



